Motivation

Instead of updating factor graph at a high frequency, condense a sereis of IMU measurements into a single factors between two poses X1 and X2.

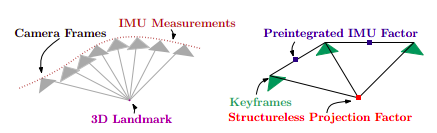
Formulation

The IMU sensory noise can be parameterized with slowly-chanding bias and gaussian noise. Specifically, the bias is modeled as random-walk noise. Combined this knowledge with the kinematic model, the change between two states could be represented as the following equations. Note that angular velocity and acceleration are assumed to be constant in the interval [t, t + dt], and that bias is assumed to be known.

Integrate in local frame

The above equations impose absolute constraint on the velocity and pose. However, as the pose (orientation) change in optimization, all the integration needs to be re-evaluated. To avoid this, the constraint is re-fomulated as a relative constraint between two states.

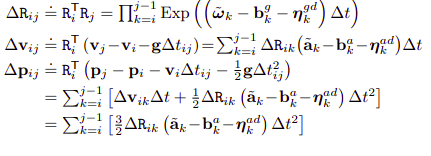
Seperate noise as additive terms

In order to meet the general assumption in SLAM literature: i.e. the measurement is true value combined with an additive Gaussian noise, the Baker-Campbell-Hausdoff approximation is used to seperate Gaussian noise in rotation as a “perturb” pose. Similiarly, the velocities and poses can be seperated.

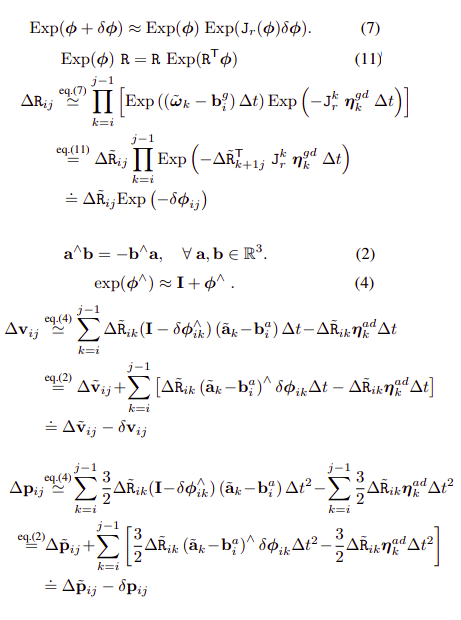
Residuals with bias update

Change in bias is updated with taylor series expansion, so the integration does not have to be re-computed. And the resiudal between measurement and prediction can thus be written as the follows.

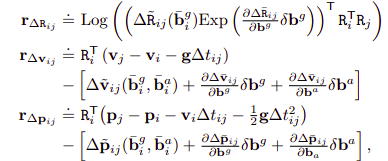
Wheares the estimation of bias is formulated as follows, with the assumption that difference between consecutive biases belongs to Gaussian distribution.

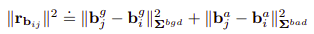
Remark

covariance of the between-state constraint and bias is much more complicated, and require reference to the original paper.