First and Second Order Gradient Descend

By approximating the formula as first order or second order talyer series, we can obtain first order or second order (newton method) algorithm respectively. Both of the approaches have their drawbacks. First order could take more time to converge (second line), second order (third line) is relative computationally expensive.

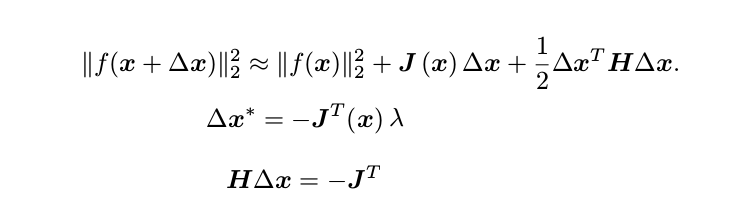
Gaussian Newton

By approximating the objective function f(x) (instead of f(x)^2 )as first order talyor series, we can obtain the expression below:

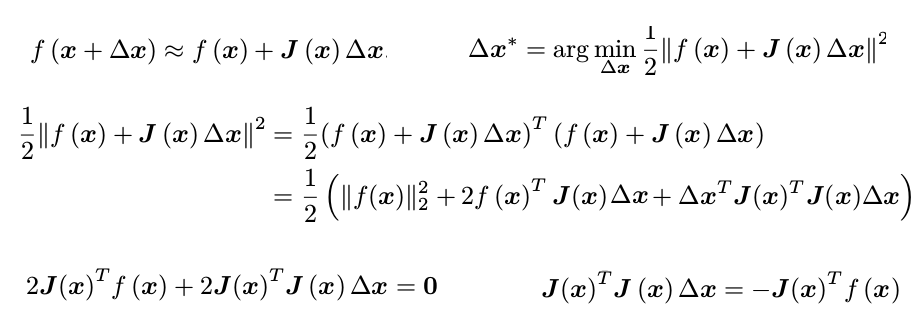
Note that we use J^T J to approximate hessian H. The drawbacks are (1) J^T J is only semi-positive definite (2) the computed delta x could be too large, which makes the approximation incorrect. Both can lead to divergence of the algorithm.

Levenberg-Marquadt

To alleviate the “quadratic is a bad approximation” issue in G-N, the regularization is introduced (also known as lagrange multiplier) to regularize delta x. When the approximation decreases slower than the actual function we believe that the quadratic is a good approximation and hence reduce lambda by a factor of 10, behaving more like gaussian newton. Otherwise, the step is reject, and lambda is increase by a factor of 10, behaving more like first order gradient descend.

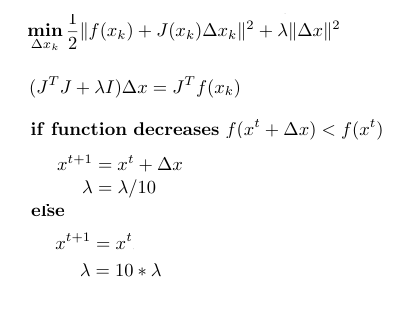
Remarks:

1. Deep learning utilize first order algorithm, since gaussian newton does not gaurantee convergence, Hessian is computationally expensive and LM is just slower.
2. Initialization is crtical for these optimization algorithms. For SLAM, it could be ICP or PnP etc.
3. It’s not always neccessary to introduce damping factor (LM). Take small pose delta_s estimated in LiDAR ICP for example, because we’re estimating delta_s starting from origin using Lie algebra, which is pretty linear around the origin, the loss surface can actually be well approximated linearly. However, for degenerated geometry such as a big flat wall (insufficient rank thus not invertible), it may then be desirable to use damping factor. In addition, bad parameterization such as euler angles (introduce singularities) may also require a damping factor for solver stability.