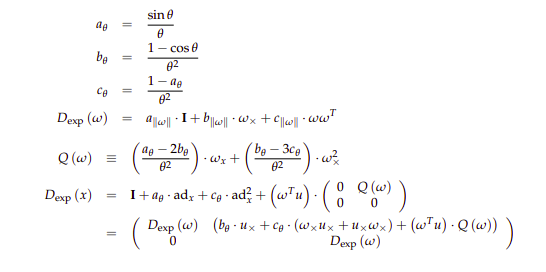Deriviative of Lie Algebra
Lie Algebra and Point Transformation
Baker-Campbell-Hausdoff Approximation
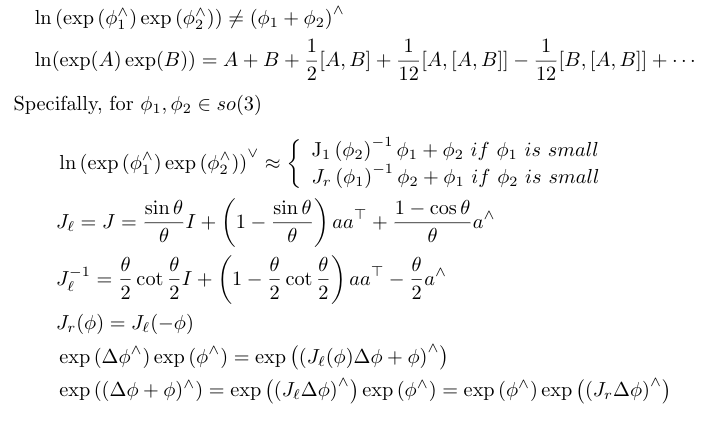
Left Pertubation Model so(3)
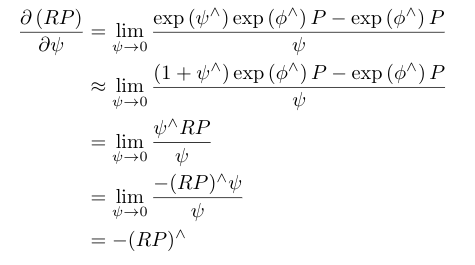
Left Pertubation Model se(3)

Lie Algebra, Jacobian and Kalman Filter
Recall in KF we have X = AX + BU. If we instead represent the 6DoF state vector using Lie algebra, then the question of which jacobian do we propagate uncertainty naturally arises. There are multiple blocks in jacobian that relates different state variables, e.g. R_t and R_t-1 or R_t and w_t-1. Here R, w represents SO(3) and angular velocity respectively.
To answer some of these questions, it’s necessary to introduce the concept of adjoint
Introduction of adjoint matrix


Deriving jacobian block for jac_R_R
With the concept of adjoint matrix, we can now derive the jacobian block R_R using the left jacobian definition:

Jacobian block for jac_R_w, jac_t_w, jac_R_v and jac_t_v
since R2 = exp(w) R1 (here w is a se(3)), diff(R2) = diff(exp(w)) R1, which has the form: