Motivation

In pose optimization, often we need to incrementally update orientation. However, rotation matrices does not have a well defined addition operator. For example, given two SO(3) matrices A, B, their sum (A+B) is most likely not a member of SO(3), which demands extra constraint on the optimization process. To circumvent this, Lee Algebra provides a vector representation of SO(3), which is much easier to work with. Mathmatically, lee group forms a tangent space on the surface of SO(3). Thus, the minimum least square loss function f can be re-parameterized with tangent (delta) x and the retraction (log-map) function.

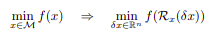
Introduction

A member of special orhogonal group SO(3) multiplies with its own transpose gives identity. Take derivative on both side, we then observed a skew symmetric matrix, whose corrisponding 1x3 vector is denoted as phi.

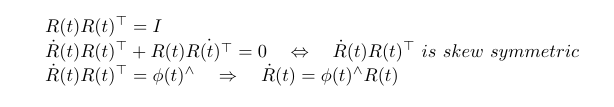
If we do a first-order taylor approximation, and let the original orientation be identity, we can obtain the following equations. Solve the ODE and we arrive at the matrix exponential form, which can be proved as a rotational matrix indeed. Note that we assume phi_{t0} be constant around t0, thus this solution only holds when t is sufficiently close to t0.

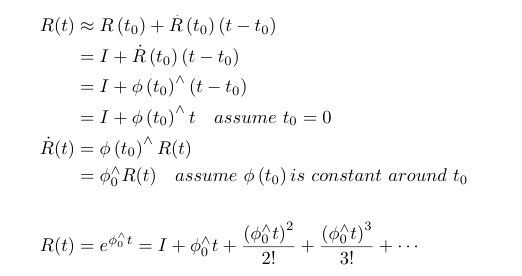
Proof Exponential Map SO(3) is Rotational Matrix

Alternative to log map

Although there’s log map from SO(3) to so(3), in pratice, the following method is easier to work with.

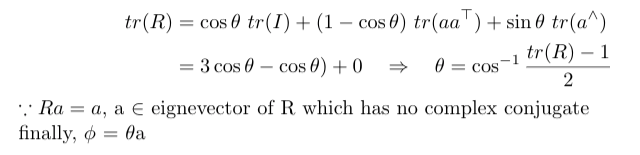
Formal Defintiion

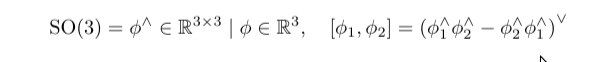
SE(3) Equations