Point-to-Point Metric (with Known Data Association)

A direct, optimal R exists for this formulation. Note the objective function is different from general Ax=b formulation but instead argmax(tr(RH)). By exploiting the orthnomal matrices U, V from SVD decomposition of H, the optimal R can be constrcuted as VU’ if det(VU’) equals to 1 i.e. VU’ is an element of SO3. The paper argued that det(VU’) equals to -1 iff noise is large. In an event where data association is unknown, points can be associated(guessed) using projective method etc as shown in kinect fusion.

Point-to-Plane Metric

Normal-based methods often converges faster and are adopted more widely in practice. But such formulation (along with other more generic error metrics) has no direct, optimal solution. It could still, however, be solved using iterative methods such as Gaussian Newton: linearizing error func wrt SE3 lie algebra and construct the normal equation Ax=b by J’J delta_x = J’ err. Alternatively, small angle assumption can also be applied, with some re-arrangement of parameters to formulate the problem as Ax = b, where delta_x is 6 DoF motion vectors.

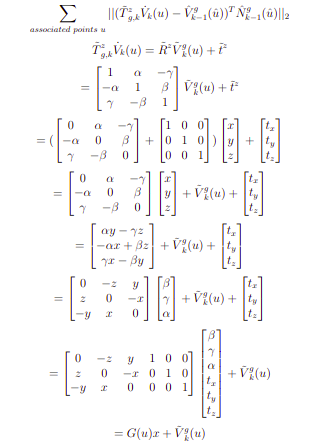
Remarks

1. Since the small angle assumption formulation is about solving “change of pose” instead of directly computing the roll, pitch and yaw angles, it avoids messing with the problem of singularities as delta_pitch should never approach singular value + or -pi/2.

Reference

1. Least Square Fitting of Two 3D Point Sets
2. Kinect Fusion
3. Cyrill Youtube Videos