Factor Graph
Diretional and Undirectional graph have their limits
Neither Bayesian nor Markov graph can fully capture conditional independence. The following graph illustrates their relationship and examples where Bayesian is a perfect while Markov isn’t and the counter example. Note that none is fully representative of joint probablistic distribution, perhaps because relationships between symbols are not just lines, but functions.
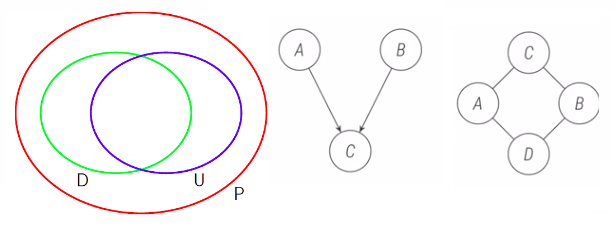
Factor Graph
Factor does not connect directly to factor, variable does not connect variable, they only connect to the other part and hence the name bipartite. The functions are meant for the computer, and the visualization of factor graph is less important since functions are just little boxes.

Remarks
- Need to figure out what exact information loses by converting Bayesian to Markov random fields